【數學力】神啊！請給我一個聖筊

數學與宗教乍看之下是光譜的兩個極端，前者用理性與邏輯來解釋各種現象，後者訴諸信仰與神祇以回答人生的大哉問。但事實上不管是東方或西方，數學與宗教之間曾出現過好幾次時下最流行的「跨領域整合」。

在歐洲，當馬丁路德推行宗教改革，造成傳統羅馬教廷權威性受到影響時，傳統的一方選擇了數學作為宗教戰爭的工具之一。他們用數學修正了當時混亂的曆法，讓信仰新宗教的人民也不得不接受，變相承認傳統教會的正統性。他們大肆宣揚數學的嚴謹邏輯觀，證明一切混亂都被驅除，自古流傳下來的規則才能替社會帶來秩序。數學如此，宗教也如此。

在東方，「宗教Ｘ數學」則合力推出了一項極受歡迎的產品——筊杯。

擲筊是一種道教信仰問卜的儀式，普遍流傳於華人民間傳統社會。「筊杯」是一種占卜工具……儀式內容是將兩個約掌大的半月形，一面平坦、一面圓弧凸出之筊杯擲出，以探測神鬼之意。

——維基百科

擲筊有4種組合：哭筊（平平）、聖筊（平凸）、聖筊（凸平）、笑筊（凸凸）。假設每種組合出現的可能性相同，則每一種的機率皆為100%/4=25%。到這邊為止都是簡單到各位看一看恐怕會心生不屑之意，覺得我在騙稿費，事實上也有一點這麼意思，還請見諒。

不過接下來就是認真的部分了。

根據行天宮的官方資料，笑筊表示信眾陳述不清，可仔細思考後重新向神明請示。

這麼一來，擲出聖筊的機率將從直覺上的50%提升到67%。

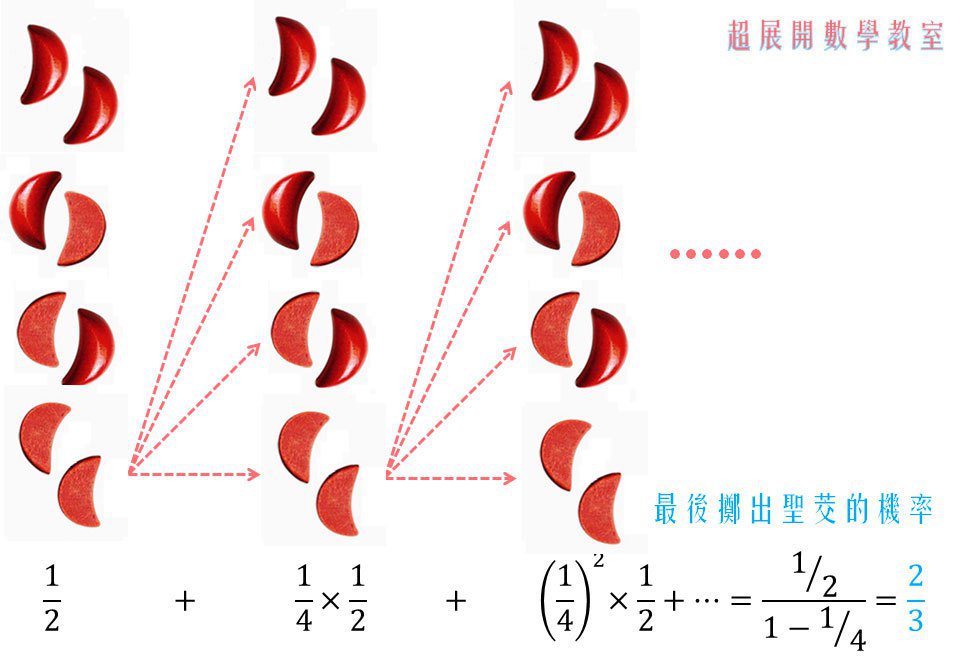
我們可以將擲筊畫成一張樹狀圖。當有人一直擲出笑筊時，樹狀圖會無限延展下去，直到擲出哭筊或聖筊。為何當笑筊代表重擲時，聖筊的機率會提升17%，來到67%呢？請看以下的分析：

第一次擲出聖筊的機率是1/2。

第一次擲出笑筊、進入第二輪的機率是1/4。

因此，「第二輪擲出聖筊」的機率便成了1/4×1/2=1/8。

共計兩輪內擲出聖筊的機率為1/2+1/8=5/8=62.5%，已經比50%提升一些了。這還沒考慮到第二輪再次擲出笑筊得繼續擲下去的狀況（神明要你多運動平常只滑手機的手腕）。

第三輪擲出聖筊的機率是：

（前兩輪都擲出笑筊的機率）×（第三輪擲出聖筊的機率）=(1/4×1/4)×1/2=1/32。

第四輪擲出聖筊的機率是：

（前三輪都擲出笑筊的機率）×（第三輪擲出聖筊的機率）=(1/4×1/4×1/4)×1/2=1/128。

依此類推下去可以得到一組「無窮等比級數」：首項a0是1/2，公比r是1/4，再利用高一上學期教的無窮等比級數和公式：

無窮等比級數和=首項/(1-公比)

帶入公式（忽然有種在當補習班老師的感覺），擲出聖筊的機率1/2+1/8+1/32+1/128+……=2/3，約是67%。

看起來跟生活毫無關聯的無窮等比級數，其實一直存在於香煙繚繞的廟宇中，庇佑著每一位善男信女。

前面的分析為了方便起見，將擲出凸面跟平面的機率設定為各50%。這樣的「方便主義假設」在數學分析中很常見，有時現實狀況太複雜，為了能掌握事物輪廓，我們會做一些簡化。簡化越多，分析結果就越簡潔明瞭、可讀性越高，得以看出參數之間的關係，但相對也會失去一些真實性。如何在「可讀性」與「真實」之中取得平衡，是數學分析中相當重要的一個課題。

不好意思有些離題了。我們回來看看，當凸面與平面機率不一樣時會發生什麼事。

我查到一篇台中縣第47屆中小學科展。科展實驗中，小學生擲筊擲了一千次筊，其中凸面次數為529次。根據筊的形狀、擲筊方式，此數據會略有變化，不過都在45%~55%之內。

有趣的是，儘管凸（平）面機率有將近10%的誤差，但對應的聖筊機率卻是穩定的49.5%~50%，只有0.5%的誤差。這是因為聖筊由凸面與平面組成，當凸面機率降低，平面機率會對應升高，導致聖筊機率相對穩定。倘若將凸面機率的變化範圍增加到30%~70%，聖筊的機率範圍依然落在42%~50%，只有8%的誤差。

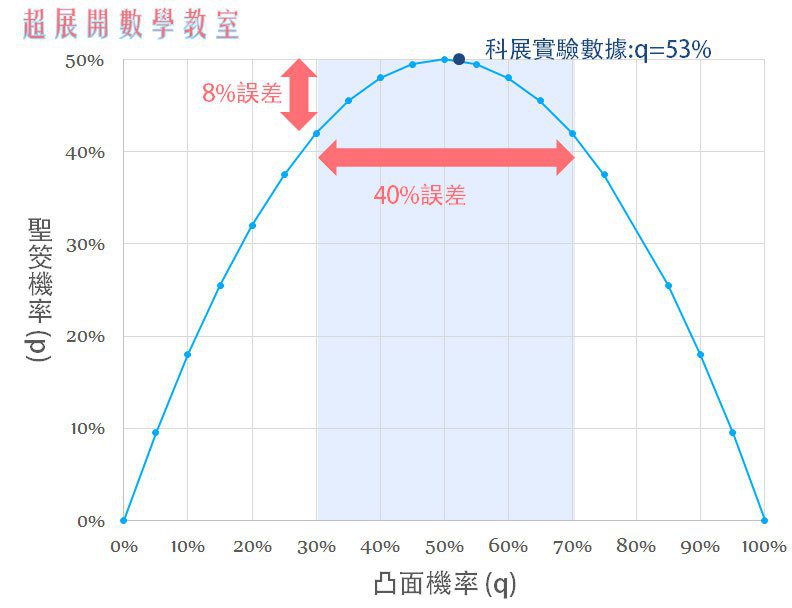
透過這樣的數學機制，不管是哪間廟的筊杯、哪種擲法都不會差太多，用不著擔心某間廟的神明特別不愛給聖筊，或廟旁開設了「擲筊補習班，幫你讓神明say yes」的狀況。

總結來說，小小的兩枚筊杯裡蘊藏了許多利用數學的巧思：透過笑筊增加聖筊的機率，讓自己請示的事情更能得到神明的肯定（前提是你得記得用正面問法，千萬不要問神明「我這次考試會被當嗎？」，否則要是神明一忙，請機率大神來幫你解惑，你就有67%的機率要帶著沉重的心情離開廟了）。一次必須擲一組兩枚的筊杯，可以有效降低筊杯製造過程、信眾擲筊手法不同帶來的誤差。

你可以說這是古人智慧，也可以說是數學之神的加持。

進階閱讀》

接下來是「算幾不等式」與「拋物線」的數學密集處，建議睡前閱讀，或供學校老師出題參考。另一個數學上的有趣之處是：聖筊機率最大值恰好出現在凸(平)面機率=50%。

我們可以用方才圖裡的拋物線，以配方法求出拋物線頂點所在。

也可以用國高中的「算幾不等式」來求。算幾不等式告訴我們，兩個數字的相乘開根號（幾何平均），小於等於兩個數字相加除以二（算術平均）。

聖筊機率=2×凸面機率×平面機率。

剛好是（凸面機率）與（平面機率）的幾何平均2倍。

幾何平均最大值發生在算幾不等式等號成立，也就是幾何平均數等於算術平均數的時候。什麼時候「兩個數字相乘開根號=兩個數字相加除以二」呢？

答案是兩個數字相等時。

換句話說，聖筊機率最大值就是發生凸面跟平面機率相等。

一副筊杯裡有等比級數、無窮、統計、機率、拋物線、算幾不等式，神明根本是數學狂熱份子。

參考資料：台中縣第四十七屆中小學科學展覽會•生活應用科•高小組《神啊！請給我一個聖筊》