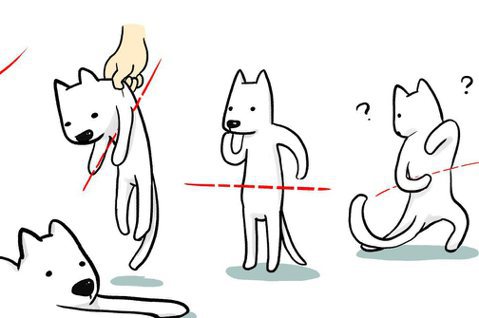
賴天恆/無限殺人遊戲

假設我是一個喜歡製造道德困境的小惡魔。1我逮住了妳,又隨機抓了另一個人,稱他為「倒霉鬼」。我跟妳說,來翻一下銅板吧:
- 妳如果翻到正面,我就把倒霉鬼放了,遊戲結束。
- 妳如果翻到反面,我就隨機殺一個倒霉鬼之外的人,然後要妳再翻銅板。
- 妳隨時可以拒絕(再)翻銅板,但只要妳拒絕,我就把倒霉鬼殺了,遊戲結束。
妳該怎麼做?
這是澳洲國立大學哲學家勒薩(Seth Lazar)在Anton's Game(2016)一文提出的思想實驗。2這個遊戲的靈感來自電影《險路勿近》(No Country for Old Man)裡,要無辜的被害人翻銅板決定生死的壞人奇哥(Anthon Chigurh)。當然,勒薩的思想實驗比電影更複雜,而且做了一些只有「無聊哲學家」才會做的假設:
- 銅板是公正的。也就是說,任何一面朝上的機率都是0.5。
- 任何被捲入的人,餘生都同樣值得活。
- 妳跟那些人沒有任何私交。
- 妳確定生死會確實按照遊戲規則判定,不會有例外或差錯。
- 有無限多的人可依序隨機被殺死。
- 妳可以做出無限多次決定。
期望值怎麼算都是死一個人?
先來看看妳的選項:
- 拒絕翻:只有倒霉鬼死。
- 翻到底:一直翻銅板翻到倒霉鬼被釋放。
- 翻個幾次:翻銅板,但最多只翻個幾次就拒絕再翻。
記得,(1)最簡單,只有倒霉鬼確定會死。(2)和(3)比較複雜。(2)的話有可能沒有任何人會死,但也有可能妳連續翻到好幾次反面,結果死了很多人。(3)的話,有可能沒有任何人會死,有可能死了幾個人後倒霉鬼得以存活,但也有可能死了幾個人後倒霉鬼最後還是死。
據說台灣大家數學都很好。3這個遊戲的期望值大家都算得出來:
- 拒絕翻:確定會死一個人,期望值就是會死一個人。
- 翻到底:銅板無限翻下去的話,死亡人數窮盡所有可能性會是0/2+1/4+2/8+3/16+…+(n-1/2^n),加起來期望值也是會死一個人。4
- 翻個幾次:這個情況可以這樣想:翻一次就拒絕再翻,死亡人數可能性是0/2+2/2,(一半機率沒人死,另一半機率隨機殺一個人再加上倒霉鬼得死,)也就是期望值一個人會死;翻兩次就拒絕再翻可能性是0/2+1/4+3/4(一半的機率沒人死,四分之一的機率隨機殺一個人,四分之一的機率隨機殺兩個人再加上倒霉鬼死),仍然是期望值一個人會死。以此類推,不管妳是決定翻幾次一定得停,期望值永遠是一個人會死。
就此而言,如果光看期望值,不管選(1)、(2)還是(3),都是一個人會死,好像就真的沒差:喜歡怎麼做就怎麼做吧。
人命不只是期望值?
等等,人命可以這樣「算」嗎?我先說勒薩給出的答案好了。勒薩認為妳該翻幾次就拒絕再翻,而理由是已經夠多人為了倒霉鬼而死了,妳已經給倒霉鬼夠多次機會了。當然,勒薩也認為說,他自己的答案並不是那篇文章的重點,重點在於雖然期望值顯示怎麼選都沒差,但大概很少人真的這樣認為。
這個落差顯示了在做道德決定時,除了期望值之外,似乎還有別的東西要納入考量。勒薩舉了一些例子:
- 我們對風險的態度是怎樣?我們想要確保最多就死一個人?最多就死幾個人?還是樂於擁抱任何風險?(如果我們對風險偏向保守的話就會選擇不翻或最多只翻幾次。)
- 我們會覺得多死幾個人之後,人數就只是個統計數字,所以每個人的死好像沒有只死一個人那麼嚴重嗎? (如果我們覺得多死幾個人就只是統計數字,大概就會傾向一直翻。)
- 我們光是讓人陷入被殺死的風險之中,是不是在道德上就得罪了人?試想妳剛好就是第一個可能被隨機殺死的人。如果我選擇翻銅板,難道不是在道德上得罪了妳?即使妳幸運活下來了,妳還是會不爽吧? (如果我們覺得讓更多人陷入死亡風險是不對的,大概就會傾向不翻。)
- 還是我們該把存活與死亡的機會,讓所有人共同承擔? (讓所有人共同承擔似乎支持一直翻,或至少多翻個幾次。)
- 想想看連續翻八十一次反面的機率有多低。承受這種被殺的機率好像也還好吧?這種超低死亡機率是不是忽略算了?我們要讓這種超低期望值影響到道德抉擇嗎? (這樣似乎會讓人覺得一直翻也沒什麼不好,因為忽略一些超低死亡機率會讓加總後期望值小於一。)
- 如果突然停下來,之前死的人不就是「白白死去」嗎? (不想讓人「白白死去」應該會讓我們堅持繼續翻下去。)
- 為了拯救倒霉鬼已經死了這麼多人了,我們還能讓更多人陷於危難嗎?(「死夠多人了」大概會讓最多只翻幾次。)
我相信還有更多的東西值得考量,而對於每個問題的不同答案,都會影響到我們會怎樣選擇。妳可以思考一下,妳覺得該怎麼選?為什麼?
無聊問題?
如同我先前所說,勒薩的思想實驗有好幾個只有「無聊哲學家」才會做的假設。舉例來說:哪來無限多個人讓我慢慢殺?確實就這個角度去看,這個思想實驗(以及許多常見的思想實驗,比方說電車難題)很無聊。
然而,正好就是在這種「幾近真空」的思想實驗室裡面,我們才能釐清我們對風險、期望值的態度是什麼,以便進一步思考道德上要怎樣把風險、期望值納入考量。勒薩認為這就跟我們切身相關。當我們選擇上街抗議,選擇改變公共衛生政策,甚至選擇發動戰爭或是否要搶救麥特戴蒙時,往往都是設法追求一些值得追求的東西。5
然而,同時我們確實也知道未來充滿不確定性。我們沒有把握這一次就會成功。我們知道失敗的代價,不只是讓我們自己灰頭土臉,更可能會殃及無辜。
我們能夠嘗試幾次?或更重要地,我們該(不斷)嘗試嗎?
- 我們就暫時不追究這個假設是否正確。
- LAZAR, S. (2016). Anton's Game: Deontological Decision Theory for an Iterated Decision Problem. Utilitas, 1-22。
- 我想我一定是例外。
- 就這樣想:翻一次的話有一半的機率沒人會死(所以整體來說有一半的機率沒人死),但有一半的機率會死一個人然後得再玩一次。到了第二次,有一半的機率已經死的那個人死就死了,但正面朝上所以遊戲結束(所以整體來說有四分之一的機率遊戲就這樣結束,死一個人),但有一半的機率會再死一個人然後得再繼續玩。以此類推。
- 探討搶救麥特戴蒙的文章多半集中在花費。然而,更值得探討的,則是為了搶救麥特戴蒙,我們陷多少人於危險之中。舉例來說,我們可以思考一下火星搶救麥特戴蒙。他們讓五個人陷入死亡的風險當中,為的是一個很有可能會失敗的救援。我們也可以思考一下二戰搶救麥特戴蒙。他們讓大概一個班的士兵陷入死亡的風險中,而且確實還死了好幾個。這種場景絕對不只出現在電影當中。任何的救援任務、任何的公共衛生政策等等,都會讓一些可能沒有參與決策的人,承受一些風險。